bài viết này sẽ nói về hai phần, phần đầu tiên đề cập đến khái niệm độ lệch và kurtosis, phần thứ hai đề cập đến hai bài kiểm tra phân phối chuẩn được sử dụng nhiều nhất

Trước tiên, chúng ta nói về hình dạng của phân phối. Hình dạng của bất kỳ phân phối nào có thể được mô tả bằng hai thước đo: độ lệch và độ lệch. Như bạn thấy, phân phối chuẩn là đồng nhất, như hình dưới đây, hai chỉ số này sẽ đo mức độ “lệch, lệch phải, trái, lên xuống …” so với hình dạng của phân phối chuẩn.
chỉ số kurtosis là gì?
giá trị kurtosis: Đo lường đỉnh hoặc độ phẳng của phân phối so với phân phối chuẩn. giá trị dương biểu thị phân phối đỉnh tương đối và giá trị âm biểu thị phân phối tương đối bằng phẳng. các phân bố cao hơn hoặc nhọn hơn phân bố bình thường được gọi là leptokurtic, trong khi những phân bố bằng phẳng hơn được gọi là Platykurtic.

không đối xứng là gì?
trong khi kurtosis đề cập đến chiều cao của phân phối, độ lệch được sử dụng để mô tả sự cân bằng của phân phối; tức là nó không cân xứng và lệch về một phía (phải hoặc trái) hay nó có trọng tâm và đối xứng có hình dạng giống nhau về hai phía? nếu phân phối không cân bằng, nó sẽ bị lệch. độ lệch dương biểu thị phân phối dịch sang trái, trong khi độ lệch âm phản ánh phân phối dịch chuyển sang phải

Các giá trị độ lệch và kurtosis của phân phối chuẩn luôn bằng 0, vì vậy các giá trị trên hoặc dưới 0 hóa ra hoàn toàn khác với phân phối chuẩn.
vậy cách kiểm tra phân phối chuẩn:
Các nhà nghiên cứu có một số cách tiếp cận khác nhau để đánh giá các phân phối bình thường, nhưng chúng có thể được phân loại chủ yếu dưới dạng đồ họa hoặc thống kê. các phương pháp đồ họa được phát triển để cho phép đánh giá sự chuẩn hóa của các phân phối mà không cần tính toán phức tạp. chúng cung cấp cho nhà nghiên cứu một cái nhìn “sâu sắc” hơn về các đặc điểm phân bố so với một giá trị định lượng duy nhất, nhưng chúng cũng bị hạn chế trong việc tạo ra các phân biệt cụ thể do các diễn giải trực quan kém chính xác hơn các phép đo thống kê.
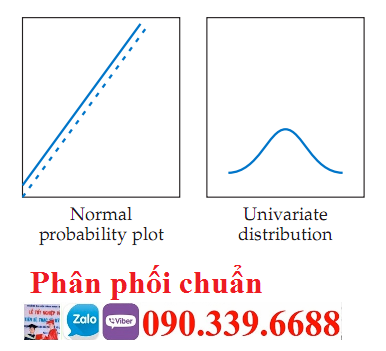
phân tích biểu đồ để xác định phân phối chuẩn
Thử nghiệm chẩn đoán chuẩn mực đơn giản nhất là kiểm tra trực quan biểu đồ so sánh các giá trị dữ liệu quan sát được với phân phối gần đúng với phân phối chuẩn. Mặc dù hấp dẫn vì tính đơn giản của nó, phương pháp này có vấn đề đối với các mẫu nhỏ, trong đó việc xây dựng biểu đồ có thể làm sai lệch hình ảnh mô tả, dẫn đến phân tích vô ích. một cách tiếp cận đáng tin cậy hơn là biểu đồ xác suất chuẩn, so sánh phân phối tích lũy của các giá trị dữ liệu thực với phân phối tích lũy của phân phối chuẩn. phân phối chuẩn tạo thành một đường chéo thẳng và các giá trị dữ liệu được vẽ trên đồ thị được so sánh với đường chéo. nếu phân phối bình thường, đường cong phân phối dữ liệu thực tế sẽ theo sát đường chéo.
kiểm tra thống kê để xác định phân phối chuẩn
một quy tắc kiểm tra bình thường đơn giản dựa trên các giá trị độ lệch và kurtosis. thống kê z độ nghiêng được tính như sau:
z = tenswness / (sqrt (6 / n)) , trong đó n là kích thước mẫu.
Thống kê z cho kurtosis được tính như sau:
z = kurtosis / (sqrt (24 / n)) , trong đó n là kích thước mẫu.
bất kỳ giá trị z nào ở trên vượt quá giá trị tới hạn, thì phân phối được xác định là không bình thường. giá trị tới hạn của phân phối z dựa trên mức ý nghĩa thống kê mà chúng tôi đề xuất. các giá trị phổ biến là + -2,58 (với mức ý nghĩa 10%) và + -1,96 (với mức ý nghĩa 5%).
Hai phương pháp thử nghiệm khác cho phân phối chuẩn là thử nghiệm shapiro-wilks và thử nghiệm kolmogorov-smirnov đã được sửa đổi. mỗi phép thử cho một mức ý nghĩa thống kê so với phân phối chuẩn. lưu ý rằng nếu kích thước mẫu nhỏ hơn 30, các thử nghiệm này cho con số không chính xác.
vì vậy tốt hơn hết bạn nên kết hợp 2 phương pháp vẽ đồ thị và kiểm tra thống kê để xác định xem phân phối có tuân theo phân phối chuẩn hay không.

