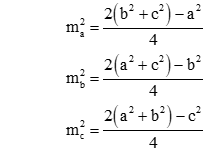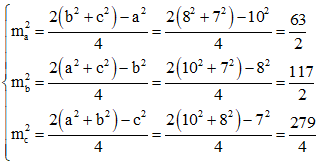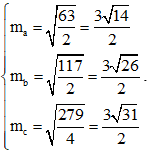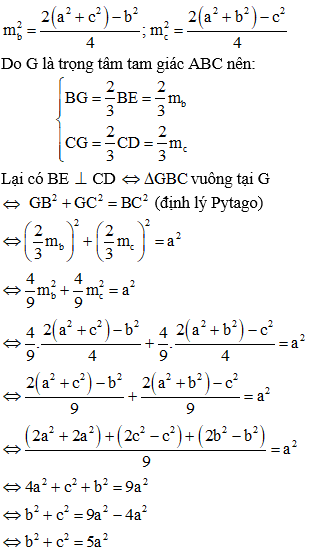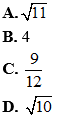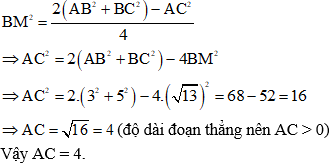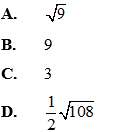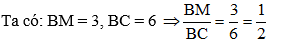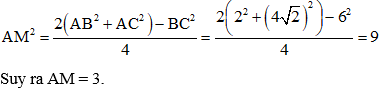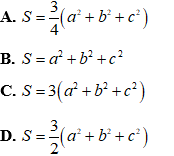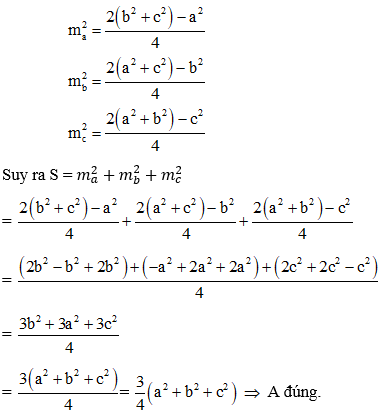Công thức, cách tính độ dài đường trung tuyến cực hay, chi tiết
Công thức, cách tính độ dài đường trung tuyến cực hay, chi tiết
A. Phương pháp giải
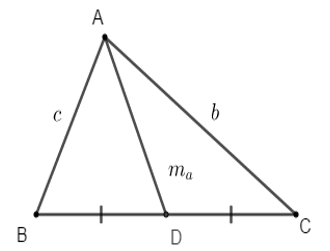
Áp dụng công thức tính độ dài đường trung tuyến:
Cho tam giác ABC có các cạnh BC = a, CA = b và AB = c. Gọi ma; mb; mc là độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A, B và C của tam giác. Khi đó
B. Ví dụ minh họa
Bạn đang xem: Công thức tính đường trung tuyến
Ví dụ 1: Cho tam giác ABC có BC = a = 10 cm, CA = b = 8 cm, AB = c = 7 cm. Tính độ dài các đường trung tuyến của tam giác ABC.
Hướng dẫn giải:
Gọi độ dài trung tuyến từ các đỉnh A, B, C của tam giác ABC lần lượt là ma; mb; mc.
Áp dụng công thức trung tuyến ta có:
Vì độ dài các đường trung tuyến (là độ dài đoạn thẳng) nên nó luôn dương, do đó:
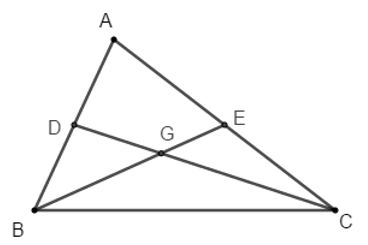
Ví dụ 2: Cho tam giác ABC, có BC = a, CA = b và AB = c. Chứng minh rằng nếu b2 + c2 = 5a2 thì hai trung tuyến kẻ từ B và C của tam giác vuông góc với nhau.
Hướng dẫn giải:
Gọi D và E lần lượt là trung điểm của AB và AC, G là trọng tâm tam giác ABC.
Đặt BE = mb, CD = mc
Áp dụng công thức trung tuyến trong tam giác ABC ta có:
Vậy b2 + c2 = 5a2 thì hai trung tuyến kẻ từ B và C của tam giác vuông góc với nhau. (đpcm)
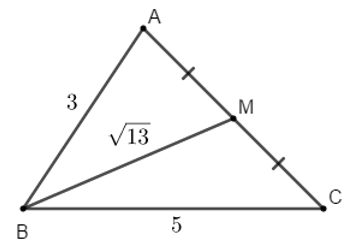
Ví dụ 3: Cho tam giác ABC có AB = 3, BC = 5 và độ dài đường trung tuyến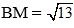 
. Độ dài AC là:
Hướng dẫn giải:
BM là trung tuyến của tam giác ABC, áp dụng công thức trung tuyến ta có:
Đáp án B
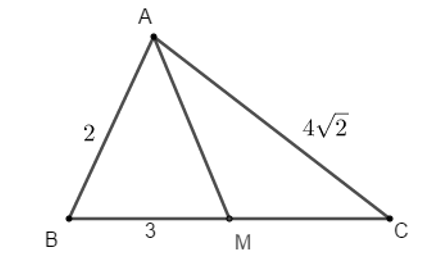
Ví dụ 4: Tam giác ABC có BC = 6, AC =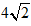 
, AB = 2. M là một điểm trên cạnh BC sao cho BM = 3. Giá trị của AM là?
Hướng dẫn giải:
Mà M thuộc BC.
Do đó M là trung điểm của BC => AM là trung tuyến của tam giác ABC, áp dụng công thức trung tuyến ta có.
Đáp án C
Ví dụ 5: Gọi S = ma2 + mb2 + mc2 là tổng bình phương độ dài ba đường trung tuyến của tam giác ABC. Khẳng định nào sau đây là đúng? (cho BC = a, CA = b, AB = c)
Hướng dẫn giải:
Áp dụng công thức trung tuyến trong tam giác ABC ta có:
Đáp án A
Xem thêm các dạng bài tập Toán lớp 10 chọn lọc, có đáp án hay khác khác:
- Cách chứng minh Hai vecto vuông góc cực hay, chi tiết
- Tìm m để góc giữa hai vecto bằng một số cho trước cực hay (45 độ, góc nhọn, góc tù)
- Cách giải bài tập về Định lí Cô-sin trong tam giác cực hay, chi tiết
- Cách giải bài tập về Định lí Sin trong tam giác cực hay, chi tiết
- Công thức, cách tính Diện tích tam giác cực hay, chi tiết
Giới thiệu kênh Youtube VietJack
Ngân hàng trắc nghiệm lớp 10 tại httl.com.vn
- Hơn 7500 câu trắc nghiệm Toán 10 có đáp án
- Hơn 5000 câu trắc nghiệm Hóa 10 có đáp án chi tiết
- Gần 4000 câu trắc nghiệm Vật lý 10 có đáp án
